最优化问题的一般形式：

（重要性质：凸问题的可行集为凸集）

（定理）局部和全局极小：凸优化问题的任意局部极小点都是全局最优的。

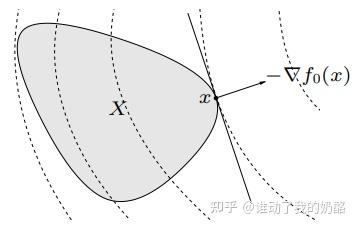
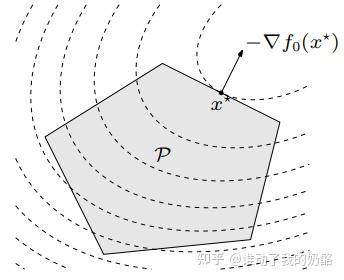
可微凸优化问题的最优性条件： 是凸优化问题 最优解，当且仅当 可行且满足：

线性规划问题的一般形式如下：

实际应用中，其他形式都可转化成两种特殊的形式：标准形式

通常假设系数矩阵 行满秩，即 。

若线性规划中包含无符号要求的决策变量 ，可引入两个非负变量 ， ，并用 代替 。

如果文中具有不等式约束 ，可引入非负松弛变量 将其等价表示为

不等式形式

若 为（正定）半正定矩阵，则该问题为（严格）凸二次规划（convex quadratic programming）。

目标函数是二次的

半定规划问题的一般形式如下：

（ 表示正定， 表示半正定）

半定规划（SDP）是线性规划在矩阵空间中的一种推广。不同的地方是，其自变量取值于半正定矩阵空间。

一般形式的优化问题都可以转化为以下标准形式

和对偶形式

可表示为以下形式：

其中，正则项 用来保证解的某种性质。 表示样本 上的损失或者奖励，该变量的数学期望 通常不可计算。为了得到目标函数值的一个比较好的估计，在实际问题中，往往利用 的经验分布来替代其真实分布。具体地，假设N个样本 ，令 ，得到优化问题

并称其为经验风险极小化问题或者采样平均极小化问题。该类问题难以求解的点在于，样本数量较多，优化问题的可行域所在空间维数较大。

未完待续

· · ·

矩阵优化问题

本文所使用的图片参考北京大学开设的凸优化课程的官方教材及《最优化基础理论与方法（第二版）》。